Rope & SumTree

在 Zed 解码 系列的第二篇文章中，我们深入探讨了 Zed 的构建方式，我与 Zed 的三位联合创始人——Nathan、Max、Antonio——讨论了 Zed 核心的数据结构：rope（绳索）。

伴随视频

Rope & SumTree

这篇博文附带一个时长 1 小时的配套视频，其中 Thorsten、Nathan、Antonio 和 Max 使用 Zed 演示了 Zed 如何使用 Rope 和 SumTree 类型。这是一场轻松的对话，我们编写并阅读了大量代码，以了解 Zed 中的 rope 如何工作和实现。

在此观看视频 →

我一开始就知道，用于表示文本的数据结构是文本编辑器领域的热门话题。我也在 Zed 代码库中使用了 Rope 类型，并且对 ropes 有一些了解。

我真正不理解的是 Zed 的 rope 如何实现以及这种实现带来了什么。所以我向 Nathan、Max 和 Antonio 询问了这个问题。他们多年来一直在 rope 的上层、下层和内部编写代码。结果发现，Zed 的 rope 实际上并不是传统意义上的 rope。它非常令人印象深刻，但首先：什么是 rope？

为什么不用字符串？

文本编辑器最重要的任务之一是在内存中表示文本。当你在文本编辑器中打开一个文件时，你希望看到它的内容并能够在其间导航，而且——没错，名字就是这么来的——你还希望能够编辑文本。

为此，文本编辑器必须将文件内容加载到内存中——你不能让用户盯着磁盘上的原始字节。你也希望将其保留在内存中，因为并非每个更改都应立即保存到磁盘。

所以问题是：如何在内存中表示文本？

我的第一个天真选择是使用字符串。老朋友字符串。我们刚开始编程时的最好朋友。为什么不用字符串呢？我们总是这样在内存中表示文本。这并不是一个显而易见的糟糕选择，对吧？

嘿，我敢打赌你确实可以用字符串做很多事情，但是字符串有一些问题，阻止它们成为最佳选择，特别是当你开始处理大文件并希望你的程序仍然高效和响应时。

字符串的问题

字符串通常被分配为连续的内存块。这会使得编辑效率低下。假设你有一个包含 2 万行的文件存储在一个字符串中，并且你想在字符串中间插入一个单词。为了做到这一点，你必须在字符串中间为新单词腾出空间，这样你仍然会得到一个连续内存块的字符串。为了腾出空间，你必须移动新插入单词之后的所有文本。这里的移动实际上意味着重新分配内存。在最坏的情况下，你必须移动所有内容——所有 2 万行——来为新单词腾出空间。

或者说你想删除一个单词：你不能简单地在字符串中“挖一个洞”，因为那样它就不再是一个字符串——一个连续的内存块。相反，你必须移动除了你删除的字符之外的所有字符，这样你就能再次得到一个单一的连续内存块，这次没有被删除的单词。

在处理小文件和短字符串时，这些都不是问题。我们每天都在做类似的字符串操作，对吧？是的，但大多数时候我们谈论的是相对较小的字符串。当你处理大文件，从而处理大字符串或大量编辑（甚至可能是同时进行——多光标你好！）时，这些事情——内存分配、内存中字符串的移动——就会成为问题。

这甚至还没有触及文本编辑器可能对其文本表示提出的所有其他要求。

例如，导航。如果用户想跳转到第 523 行怎么办？使用字符串且没有任何其他数据，你必须逐个字符地遍历字符串，并计算其中的换行符以找出第 523 行在字符串中的位置。如果用户向下按箭头十次以向下移动十行并希望停留在同一列怎么办？你将不得不再次开始计算字符串中的换行符，然后找到最后一个换行符后的正确偏移量。

或者，假设你想在编辑器底部绘制一个水平滚动条。要了解滚动条的大小，你必须知道文件中最长行的长度。同样，你必须遍历字符串并计算行数，这次还要跟踪每行的长度。

或者，如果想加载到编辑器中的文本文件大于 1GB，而你用来实现文本编辑器的语言只能表示小于 1GB 的字符串怎么办？你可能会说“1GB 的字符串应该足够所有人使用”，但这只能说明你还没有与足够的文本编辑器用户交流过。

玩笑归玩笑，我想我们已经确定字符串可能不是在文本编辑器中表示文本的最佳解决方案。

那么我们还能用什么呢？

什么比字符串更好？

如果你真的喜欢字符串，你现在可能会想“比字符串更好？简单：多个字符串。”你说得没错！有些编辑器确实将文本表示为行数组，其中每行都是一个字符串。VS Code 的Monaco 编辑器在很长一段时间里都是这样工作的，但字符串数组仍然会受到与单个字符串相同的问题困扰。过度的内存消耗和性能问题让 VS Code 团队寻找更好的解决方案。

幸运的是，有比字符串更好的东西。文本编辑器的开发者们早已意识到字符串并非这项工作的最佳工具，并提出了其他数据结构来表示文本。

据我所知，最受欢迎的是间隔缓冲区、段表和绳索。

它们各有优缺点，我在这里不做详细比较。只需知道它们都明显优于字符串，并且不同的编辑器在面对不同的权衡时做出了不同的决定，最终采用了不同的数据结构。举个例子：Emacs 使用间隔缓冲区，VS Code 使用一种改进的段表，Vim 有自己的树状数据结构，Helix 使用绳索。

Zed 也使用绳索。所以让我们来看看绳索，看看它比字符串有什么优势。

绳索 (Ropes)

维基百科是这样解释绳索的：

绳索是一种二叉树，其中每个叶子（末端节点）包含一个字符串和长度（也称为“权重”），树中更上层的每个节点则包含其左子树中所有叶子长度的总和。

绳索不是连续的内存块，而是一棵树，其叶子是它所代表文本的字符。

文本 "This is a rope" 在绳索中的样子如下

你现在可能觉得这比字符串复杂得多，你说得没错——确实如此。但这里是让绳索在许多情况下胜过字符串的关键之处：叶子——"This", " is ", "a ", "rope"——本质上是不可变的。你修改的不是字符串，而是修改树。你不是在字符串中挖洞并移动内存中的部分，而是修改树以获得一个新的字符串。到目前为止，我们程序员已经找到了如何高效地使用树的方法。

让我们再次使用上面的例子：删除文本中某个位置的单词。使用字符串，你必须重新分配单词之后的所有文本，甚至可能是整个字符串。使用 rope，你找到要删除单词的起始和结束位置，然后在这两个位置分割树，这样你就有了四棵树，你扔掉中间两棵树（只包含被删除的单词），连接另外两棵，然后重新平衡树。是的，这听起来很多，而且它确实需要在底层进行一些算法上的精细操作，但内存和性能相比字符串有非常真实的改进：你只需更新几个指针，而不是在内存中移动东西。这对于像"This is a rope"这样短的文本来说可能看起来很傻，但当你处理非常大的文本时，它会带来巨大的好处。

我知道这很抽象，所以让我展示给你看。我们来看看 Zed 的 rope 实现。

Zed 的 rope 实现

Zed 在其自己的 crate 中实现了自己的绳索：rope。（Zed 之所以有自己的实现而不是使用库，原因之一是 Zed 创始人在 2017 年奠定基础时，许多库还不存在。）

rope crate 中的主要类型是 Rope。以下是它的使用方式

let mut rope = Rope::new();
rope.push("Hello World! This is your captain speaking.");

到目前为止，与 String 类似。现在假设我们有两个 rope

let mut rope1 = Rope::new();
rope1.push("Hello World!");
 
let mut rope2 = Rope::new();
rope2.push("This is your captain speaking.");

如果我们要连接它们，只需这样做

rope1.append(rope2);
 
assert_eq!(
    rope1.text(),
    "Hello World! This is your captain speaking.".to_string()
);

调用 rope1.append 通过构建一棵包含两棵树的新树来连接 rope1 和 rope2。这几乎只是更新几个指针而已。将其与字符串进行比较：如果你连接两个字符串，你至少需要将其中一个移动到内存中，使它们相邻，形成一个连续的块。通常你需要移动它们两个，因为第一个字符串后面没有足够的空间。再次强调：此示例中的文本短得可笑，但如果有人想在一个文件中包含 2.5 万行 SQLite amalgamation 的十个副本怎么办？

替换一个词怎么办？

// Construct a rope
let mut rope = Rope::new();
rope.push("One coffee, please. Black, yes.");
 
// Replace characters 4 to 10 (0-indexed) with "guinness".
rope.replace(4..10, "guinness");
assert_eq!(rope.text(), "One guinness, please. Black, yes.");

幕后发生了什么

• replace() 创建了一个新的 rope，它包含原始 rope 的所有节点，直到第 5 个字符 (c)
• 新文本 guinness 追加到新的 rope 中
• 原始 rope 的其余部分，即字符 11 之后的所有内容，都附加到新的 rope 中

删除一个单词？只需用 "" 替换它

let mut rope = Rope::new();
rope.push("One coffee, please. Black, yes.");
rope.replace(4..10, "");

即使处理大量文本，这些操作也非常快，因为树中的大多数节点都可以重用，只需重新连接。

但是被删除的单词 "coffee" 发生了什么呢？包含这些字符的叶节点一旦不再被其他节点引用，就会被自动清理。这就是 rope 中不可变叶节点所带来的好处：当 rope 被修改，或者从旧 rope 构造出新 rope，或者两个 rope 合并成一个新 rope 时，本质上改变的只是对叶节点的引用。这些引用被计数：一旦不再有对节点的引用，节点就会被清理，释放内存。

更准确地说，从技术角度来看：在 Zed 的绳索实现中，叶节点（包含实际文本的节点）并非完全不可变。这些叶节点有一个最大长度，如果，比如说，文本被追加到绳索中，并且新文本足够短，可以容纳到最后一个叶节点中而不超过其最大长度，那么该叶节点将被修改，文本将追加到其中。

然而，从概念层面来看，你可以将绳索视为一种持久性数据结构，其节点是树中具有引用计数的不可变节点。这使其成为比字符串更好的选择，并让我们回到之前跳过的问题：为什么 Zed 选择绳索而不是其他数据结构？

Zed 为什么要使用绳索？

Zed 的目标是成为一款高性能的代码编辑器。正如我们所看到的，字符串无法让你达到高性能。那么，你该用什么呢？间隔缓冲区、绳索还是段表？

这里没有一个单一、显而易见的最佳选择。这完全取决于具体需求以及你为了满足这些需求愿意做出的权衡。

也许你听说过间隔缓冲区可能比绳索更快，或者它们更容易理解，或者段表更优雅。这可能是真的，但是这仍然不意味着它们是比，比如说，绳索更明显的选择。以下是ropey 的作者（一个流行的 Rust 绳索实现）关于绳索和间隔缓冲区之间性能权衡的论述

绳索做出了不同的性能权衡，是一种“万金油”类型。它们在任何方面都不是最好的，但它们始终保持 O(log N) 的稳定良好性能。对于只支持本地编辑模式的编辑器来说，它们不是最佳选择，因为在这种情况下它们会比间隔缓冲区（即使对于大文档）损失大量性能。但是对于鼓励非本地化编辑的编辑器，或者只是想在这方面获得灵活性的编辑器来说，它们是一个很好的选择，因为它们始终具有良好的性能，而间隔缓冲区在不利的编辑模式下性能会急剧下降。

绳索“在任何方面都不是最好的，但它们始终保持良好”。这取决于你想要做什么，或者你希望你的编辑器能够做什么。

那么，如果你真的想利用 CPU 的所有核心呢？在“文本对决：间隔缓冲区 vs. 绳索”一文中，并发性在最后一段被提及

绳索除了性能良好之外还有其他优点。Crop 和 Ropey（注：两者都是 Rust 中的绳索实现）都支持来自多个线程的并发访问。这允许你拍摄快照以进行异步保存、备份或多用户编辑。这是使用间隔缓冲区无法轻易实现的功能。

在配套视频中，你可以听到 Max 对这一段的评论：“是的，它比所有其他东西都重要。” Nathan 补充说，“我们到处都使用它”，这里的“它”指的是并发访问、快照、多用户编辑和异步操作。

换句话说：对缓冲区中文本的并发访问是 Zed 的一个硬性要求，这就是为什么 rope 最终成为首选。

以下是一个并发访问文本在 Zed 中根深蒂固的例子：当你在 Zed 中编辑一个缓冲区并启用语法高亮时，缓冲区的文本内容快照会被发送到一个后台线程，在该线程中使用 Tree-sitter 重新解析。这在每次编辑时都会发生，并且非常非常快速高效，因为快照不需要完全复制文本。所有需要做的就是增加引用计数，因为 Zed 的 rope 中节点的引用计数是用 Arc（Rust 的“线程安全引用计数指针”）实现的。

这引出了最重要的一点：Zed 的绳索是如何实现的。因为它并不是像你在维基百科上看到的经典绳索那样实现的，而且它的实现赋予了 Zed 的绳索某些其他绳索实现可能不具备的特性，正是这种实现让绳索超越了其他数据结构。

它不是绳索，而是 SumTree

Zed 的绳索不是经典的二叉树绳索，它是一个 SumTree。如果你打开 Zed 的 Rope 定义，你会发现它不过是 Chunk 的 SumTree

struct Rope {
    chunks: SumTree<Chunk>,
}
 
struct Chunk(ArrayString<{ 2 * CHUNK_BASE }>);

一个 Chunk 是一个 ArrayString，它来自 arrayvec crate，允许内联存储字符串，而不是在堆上的其他位置。这意味着：一个 Chunk 是字符的集合。Chunk 是 SumTree 中的叶子，最多包含 2 * CHUNK_BASE 个字符。在 Zed 的发布版本中，CHUNK_BASE 是 64。

那么 SumTree 是什么？问 Nathan，他会说 SumTree 是“Zed 的灵魂”。但对 SumTree 更技术性的描述是这样的

一个 SumTree<T> 是一个 B+ 树，其中每个叶节点包含多个类型为 T 的项，以及每个 Item 的 Summary。内部节点包含其子树中项的 Summary。

以下是与之匹配的类型定义，你可以在 sum_tree crate 中找到

struct SumTree<T: Item>(pub Arc<Node<T>>);
 
enum Node<T: Item> {
    Internal {
        height: u8,
        summary: T::Summary,
        child_summaries: ArrayVec<T::Summary, { 2 * TREE_BASE }>,
        child_trees: ArrayVec<SumTree<T>, { 2 * TREE_BASE }>,
    },
    Leaf {
        summary: T::Summary,
        items: ArrayVec<T, { 2 * TREE_BASE }>,
        item_summaries: ArrayVec<T::Summary, { 2 * TREE_BASE }>,
    },
}
trait Item: Clone {
    type Summary: Summary;
 
    fn summary(&self) -> Self::Summary;
}

那么 Summary 是什么？任何你想要的！唯一的要求是，你必须能够将多个摘要相加，以创建一个摘要的总和。

trait Summary: Default + Clone + fmt::Debug {
    type Context;
 
    fn add_summary(&mut self, summary: &Self, cx: &Self::Context);
}

但我知道你对此不屑一顾，所以让我们具体一点。

由于 Rope 是一个 SumTree，并且 SumTree 中的每个项目都必须有一个摘要，因此以下是与 Zed 的 Rope 中的每个节点关联的 Summary

struct TextSummary {
    /// Length in UTF-8
    len: usize,
    /// Length in UTF-16 code units
    len_utf16: OffsetUtf16,
    /// A point representing the number of lines and the length of the last line
    lines: Point,
    /// How many `char`s are in the first line
    first_line_chars: u32,
    /// How many `char`s are in the last line
    last_line_chars: u32,
    /// How many UTF-16 code units are in the last line
    last_line_len_utf16: u32,
    /// The row idx of the longest row
    longest_row: u32,
    /// How many `char`s are in the longest row
    longest_row_chars: u32,
}

SumTree 中的所有节点——内部节点和叶节点——都有这样的摘要，其中包含有关其子树的信息。叶节点有其 Chunk 的摘要，内部节点则有一个摘要，它是其子节点摘要的总和，递归地向下到树的底部。

假设我们有以下文本

Hello World!
This is
your captain speaking.
Are you
ready for take-off?

5 行文本。如果将其推入 Zed Rope，则 Rope 下方的 SumTree 将简化为如下所示

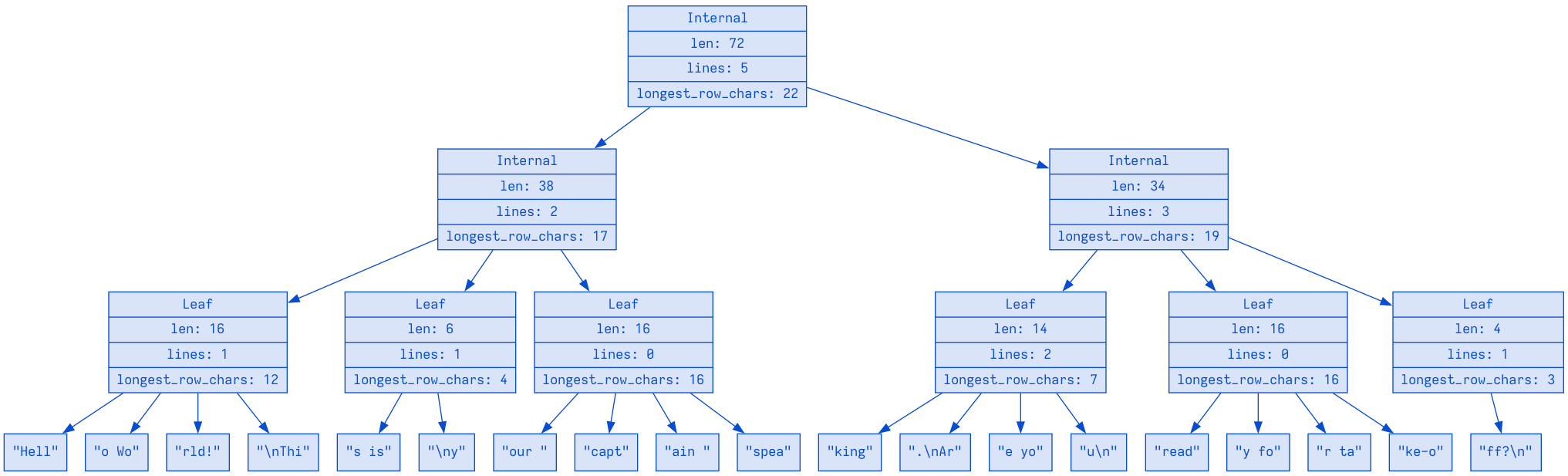
（我省略了 TextSummary 的一些字段，以使图表保持较小，并调整了块的最大大小和每个节点的最大子节点数。在 Zed 的发布版本中，所有五行文本都将适合单个节点。）

即使只有三个摘要字段——len、lines、longest_row_chars——我们也可以看到内部节点的摘要是其子节点摘要的总和。

根节点的摘要告诉我们关于完整文本、完整的 Rope 的信息：72 个字符，5 行，最长行有 22 个字符 (your captain speaking.\n)。这里的左内部节点告诉我们，例如，从 "Hell" 到 "spea" 有 38 个字符（包括换行符），并且该部分文本中有两个换行符。

好吧，你可能在想，一个带有汇总摘要的 B+ 树——这能给我们带来什么好处？

遍历 SumTree

SumTree 是一种并发友好的 B 树，它不仅为我们提供了一种持久的、写时复制的数据结构来表示文本，而且通过其摘要，它还索引了树中的数据，并允许我们以 O(log n) 的时间复杂度遍历摘要维度上的树。

用 Max 的话说，SumTree “在概念上不是一个映射。它更像是一个 Vec，具有这些特殊的索引功能，你可以存储任何你想要的项序列。你决定顺序，它只提供这些查找和切片的能力。”

不要将其视为允许您查找与键关联的值的树（尽管它可以这样做），而应将其视为允许您根据每个项目的摘要以及树中其前面所有项目的摘要查找项目的树。

或者换句话说：SumTree 中的项是有序的。它们的摘要也是有序的。SumTree 允许你通过从根节点到叶节点遍历树，并根据节点的摘要决定访问哪个节点，以 O(log N) 的时间复杂度找到树中的任何项。

假设我们有一个包含三行文本的 Rope

let mut rope = Rope::new();
rope.push("Line one.\n");
rope.push("This is the second line.\n");
rope.push("This is three.\n");

Rope 构建完成后，它看起来像这样

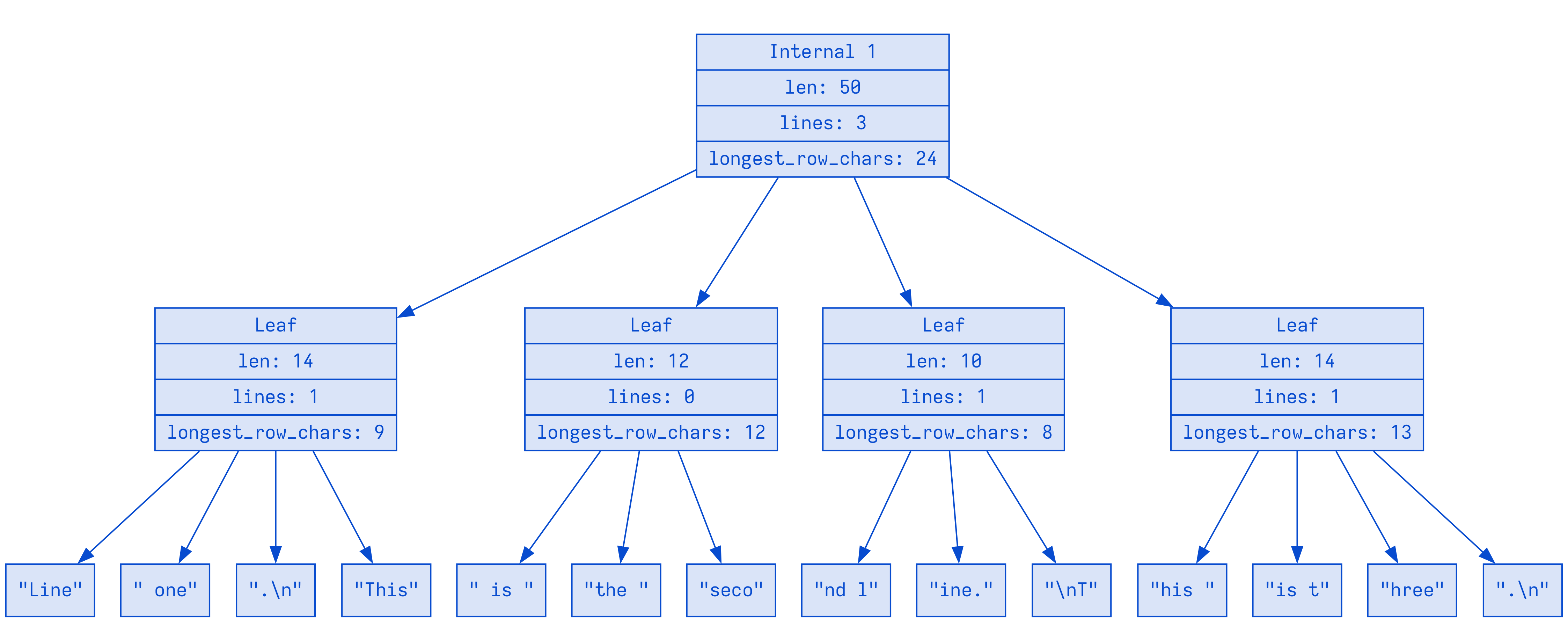
如上所述：每个叶节点将包含多个 Chunk，每个叶节点的摘要将包含其 Chunk 中文本的信息。该摘要的类型是上面提到的 TextSummary。这意味着每个节点的摘要可以告诉我们其块中文本的 len、其中的行和列、最长行以及 TextSummary 的所有其他字段。SumTree 中的内部节点然后包含摘要的摘要。

由于树中的项——内部节点、叶节点、块——是有序的，我们可以非常高效地遍历这棵树，因为 SumTree 允许我们根据摘要中的值遍历树。它允许我们沿着给定摘要的单个维度，例如单个字段，进行查找。

假设我们想知道在绝对偏移量 26 处绳索中的行和列。也就是说：字符 26 处是什么？为了找出答案，我们可以沿着 TextSummary 的 len 字段遍历这个三行 rope。因为 len 字段从左到右累加，就是一个绝对偏移量。所以为了找到绝对偏移量 26 处的内容，我们向下遍历树，向左或向右转弯，这取决于内部节点摘要中的 len 值，直到我们到达想要的叶节点

let point = rope.offset_to_point(26);
assert_eq!(point.row, 1);
assert_eq!(point.column, 16);

从表面上看，对 rope.offset_to_point(26) 的调用将一个绝对的 0 基偏移量 (26) 转换为行和列 (1 和 16)。在 offset_to_point 内部发生的是，一个光标遍历 SumTree，直到找到聚合的 TextSummary 的 len 值 >= 26 的项。一旦找到第一个满足条件的叶节点，它就会找到与偏移量匹配的确切块，并将光标停在那里。在此过程中，它不仅持续计算它遇到的摘要的 len 字段，而且还聚合了 lines 字段，其中包含 row 和 column。很酷，对吧？

我刚才描述的这些都是实际代码，这是 Rope 上的 offset_to_point 方法

fn offset_to_point(&self, offset: usize) -> Point {
    if offset >= self.summary().len {
        return self.summary().lines;
    }
    let mut cursor = self.chunks.cursor::<(usize, Point)>();
    cursor.seek(&offset, Bias::Left, &());
    let overshoot = offset - cursor.start().0;
    cursor.start().1
        + cursor
            .item()
            .map_or(Point::zero(), |chunk| chunk.offset_to_point(overshoot))
}

它执行以下操作

• 健全性检查，确保偏移量没有超出整个 Rope 的末尾
• 创建一个沿 usize（偏移量）和 Point（Point 是一个包含 row 和 column 两个字段的结构体）维度寻找的游标，同时聚合两者
• 一旦在 offset 找到一个项，它会计算超调量：我们正在寻找的 offset 可能位于单个块的中间，而 cursor.start().0 是给定块开始处的 usize（偏移量）
• 将到当前块开头的行数 (cursor.start().1) — 这是当前项左侧整个树的 TextSummary.len 的摘要！
• 将它们加到（可能在）块中间偏移量处的行中 (chunk.offset_to_point(overshoot))

这里最有趣的部分当然是使用 self.chunks.cursor::<(usize, Point)>() 构造的光标。这个特定的光标具有两个维度，允许你沿着给定 SumTree 的一个维度 (usize) 查找值，并在同一操作中获取特定光标位置处第二个维度 (Point) 的总和。

它的美妙之处在于它可以在 O(log N) 时间内完成，因为每个内部节点都包含摘要的摘要（在这种情况下意味着其子树中所有项的总 len），并且它可以跳过所有 len < 26 的节点。在上面的图中，你可以看到我们甚至不必遍历前两个叶节点。

这不是很棒吗？还有更多。

使用 SumTree

你也可以反向遍历 SumTree，沿着行/列寻找并获得最终的偏移量。

// Go from offset to point:
let point = rope.offset_to_point(55);
assert_eq!(point.row, 2);
assert_eq!(point.column, 6);
 
// Go from point to offset:
let offset = rope.point_to_offset(Point::new(2, 6));
assert_eq!(offset, 55);

而且——你可能已经猜到了——point_to_offset 看起来与 offset_to_point 完全一样，只是构造光标的维度颠倒了。

fn point_to_offset(&self, point: Point) -> usize {
    if point >= self.summary().lines {
        return self.summary().len;
    }
    let mut cursor = self.chunks.cursor::<(Point, usize)>();
    cursor.seek(&point, Bias::Left, &());
    let overshoot = point - cursor.start().0;
    cursor.start().1
        + cursor
            .item()
            .map_or(0, |chunk| chunk.point_to_offset(overshoot))
}

这种沿一个维度搜索并沿多个维度聚合（汇总！）的功能是通过一些非常巧妙的 Rust 代码实现的，我不会详细解释，但简而言之就是这样。

给定一个像下面这样的 TextSummary（我们上面已经完整地看到了），以及一个包装它的 ChunkSummary...

struct TextSummary {
    len: usize,
    lines: Point,
 
    // [...]
}
 
struct ChunkSummary {
    text: TextSummary,
}

... 我们可以将 len 和 lines 字段定义为 sum_tree::Dimensions

impl<'a> sum_tree::Dimension<'a, ChunkSummary> for usize {
    fn add_summary(&mut self, summary: &'a ChunkSummary, _: &()) {
        *self += summary.text.len;
    }
}
 
impl<'a> sum_tree::Dimension<'a, ChunkSummary> for Point {
    fn add_summary(&mut self, summary: &'a ChunkSummary, _: &()) {
        *self += summary.text.lines;
    }
}

有了这些，我们就可以为给定的 sum_tree::Dimension 或维度元组（我们上面用 (usize, Point) 就是这样做的）构造游标。

一旦构建完成，游标就可以沿着我们定义的任何 Dimension 寻找，并聚合完整的 TextSummary 或仅聚合给定摘要类型的一个 Dimension。

或者我们也可以沿着单个维度搜索，然后一旦光标找到目标就获取整个摘要。

let mut rope = Rope::new();
rope.push("This is the first line.\n");
rope.push("This is the second line.\n");
rope.push("This is the third line.\n");
 
// Construct cursor:
let mut cursor = rope.cursor(0);
// Seek it to offset 55 and get the `TextSummary` at that offset:
let summary = cursor.summary::<TextSummary>(55);
assert_eq!(summary.len, 55);
assert_eq!(summary.lines, Point::new(2, 6));
assert_eq!(summary.longest_row_chars, 24);

光标停在第 2 行中间，第 6 列，到那个位置之前，摘要中的 longest_row_chars 是 24。

这是非常非常强大的东西。简单来说：它允许我们轻松地在 UTF8 行/列和 UTF16 行/列之间进行转换，这在使用语言服务器协议 (LSP) 时有时是必需的。只需定位到 UTF8 Point 并聚合 UTF16 Points

fn point_to_point_utf16(&self, point: Point) -> PointUtf16 {
    if point >= self.summary().lines {
        return self.summary().lines_utf16();
    }
    let mut cursor = self.chunks.cursor::<(Point, PointUtf16)>();
    cursor.seek(&point, Bias::Left, &());
    // ... you know the rest ...
}

但还有更多，我可以滔滔不绝地展示更多例子，或者使用像幺半群同态这样的大词，但我将在此打住。你懂了——SumTree，一个线程安全、快照友好、写时复制的 B+ 树，功能非常强大，不仅可以用于“仅仅”文本，这就是为什么它在 Zed 中无处不在。是的，字面意义上的。

万物皆 SumTree

目前在 Zed 中有超过 20 处使用了 SumTree。 SumTree 不仅作为 Rope 的基础，还在许多不同的地方使用。项目中的文件列表是一个 SumTree。git blame 返回的信息存储在一个 SumTree 中。聊天频道中的消息：SumTree。诊断信息：SumTree。

Zed 的核心是一个名为 DisplayMap 的数据结构，它包含了关于如何显示给定文本缓冲区的全部信息——折叠在哪里，哪些行换行，内联提示显示在哪里，……——它看起来像这样

struct DisplayMap {
    /// The buffer that we are displaying.
    buffer: Model<MultiBuffer>,
    /// Decides where the [`Inlay`]s should be displayed.
    inlay_map: InlayMap,
    /// Decides where the fold indicators should be and tracks parts of a source file that are currently folded.
    fold_map: FoldMap,
    /// Keeps track of hard tabs in a buffer.
    tab_map: TabMap,
    /// Handles soft wrapping.
    wrap_map: Model<WrapMap>,
    /// Tracks custom blocks such as diagnostics that should be displayed within buffer.
    block_map: BlockMap,
    /// Regions of text that should be highlighted.
    text_highlights: TextHighlights,
    /// Regions of inlays that should be highlighted.
    inlay_highlights: InlayHighlights,
 
    // [...]
}

猜猜怎么着？所有这些都在底层使用了 SumTree，在未来的文章中我们将探讨它们，但现在我想说的是这一点

Zed 的联合创始人并没有那么决定是使用绳索而不是间隔缓冲区或段表。他们从 SumTree 开始，认识到它的强大之处，以及它如何符合 Zed 的要求，然后在此基础上构建了绳索。

绳索可能是 Zed 的核心，但借用 Nathan 的话，“SumTree 才是 Zed 的灵魂”。